Transformers are the neural architecture that underlies most of the current state-of-the-art machine translation and natural language processing in general. One of its major drawbacks is the quadratic complexity of the underlying self-attention mechanism, which in practice limits the sequence length that could be processed by Transformers. There already exist some tricks to deal with that. One of them is local sensitive hashing that was used in the Reformer architecture (see MT Weekly 27). The main idea was computing the self-attention only for hidden states that fall into the same hash function bucket. Random feature attention, a paper by DeepMind and the University of Washington, that will be presented in this year’s ICLR introduces a new way of approximating the attention computation without materializing the quadratic self-attention matrix in the memory.

The self-attention

The self-attention is conceptually the main building block of the Transformer architecture. Self-attention is the place where the sentence tokens interact with each other and where the sentence structure is processed.

In general, attention can be understood as probabilistic information retrieval. Given a query vector $q$, we want to retrieve some values $V = (v_1, \ldots, v_n)$ using some keys $K = (k_1, \ldots, k_n)$. This is done by scoring each key by comparing it with the query using the dot-product similarity. These comparison scores get normalized using the softmax function, so we have a multinomial probability distribution over the keys. These scores are then used to compute a weighted average of the values. Using formula:

\[\mathrm{softmax}(q^T K)V^T\]

Each Transformer layer contains one state (a vector) for each input token (a word or a subword). In the self-attentive layers, each vector is used as a query to retrieve information from all the remaining states. Because it might be desirable to collect different pieces of information from different states, the attention is done several times for each state, each time differently projected in so-called attention heads.

Now, it is clear that for a sentence with $n$ tokens, we need to do $n$ vector comparisons for each of the tokens, so the complexity is quadratic. GPUs can parallelize heavily parallelize the computation, but still, quadratic memory is needed to store the scores.

The random feature trick

Unlike the Reformer, the random feature trick does not change the architecture. The only thing they do is using magic from calculus and linear algebra for clever reformulation and approximation of the original formulas.

Let us get back to the self-attention equation and rewrite the equation using the definition of the softmax function:

\[\mathrm{softmax}(q^T K)V^T = \sum_i \frac{\exp(q \cdot k_i)}{\sum_j \exp (q \cdot k_j)} v_i^T\]

At this point, they use a mathematical trick from 2007. It is a theorem that says that for a function $\phi$ that is random (but always the same) transformation of a vector with some sine and cosine functions, the following holds (screenshot of Equations 2 and 3 in the paper):

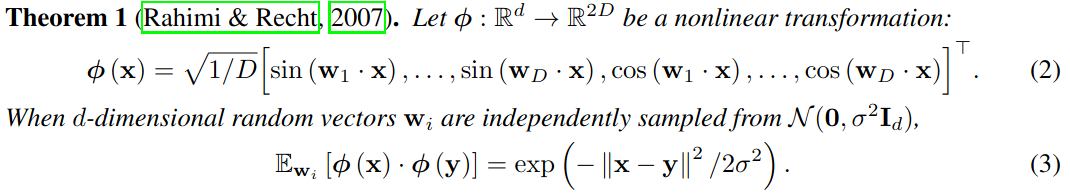
The definition of Euclidean norm says that $||x|| = \sqrt{x^T \cdot x}$. Therefore the squared difference in the theorem can be expressed,

\[||x - y||^2 = \sqrt{(x-y)^T(x-y)}^2 = x^Tx - 2x^Ty + y^Ty = ||x||^2 + ||y||^2 - 2x^Ty\]

The dot-product $xy$ can be expressed as:

\[x^T y = -||x - y||^2 / 2 + ||x||^2 / 2 + ||y||^2 / 2\]

We can substitute this in the exponentiation in the definition of the softmax and get (screenshot of Equation 4 in the paper):

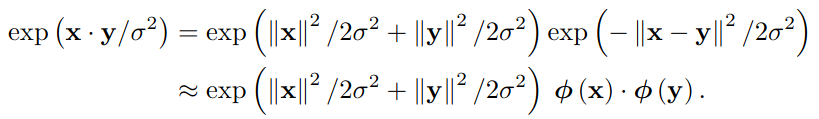
After substituting this approximation in the self-attention formula, the expressions with the norms of $\q_t$ zero out in the fraction. If we further assume that the norm of all keys is similar, we get the following (screenshot of Equation 5 in the paper):

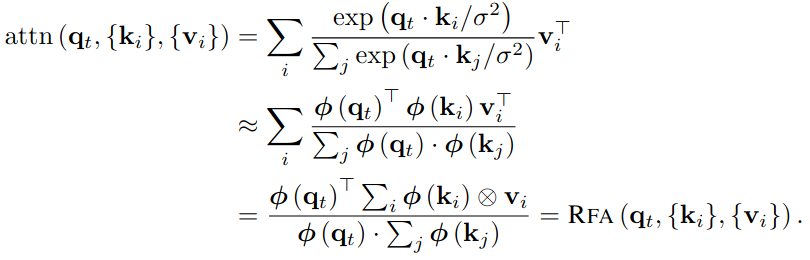
And this is it, this is the main idea of the paper. It might not be clear why it is so cool at the first sight, but it can be nicely seen in Figure 1 of the paper (it assumes we have $N$ queries and $M$ key-value pairs).

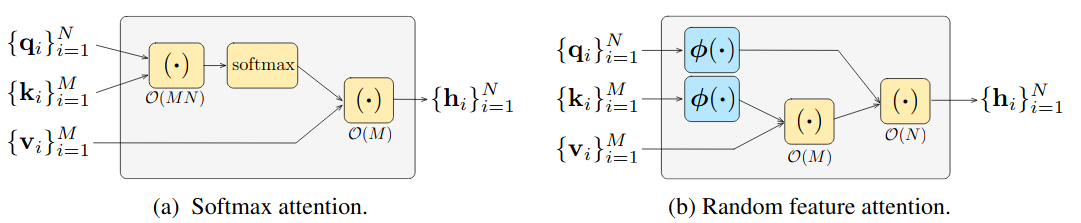
Using this trick, the intermediate results of multiplication of $Q$ and $K$, the large $M \times N$ table miraculously disappears and we get the results of the self-attention without materializing the intermediate matrix.

The other advantage of this reformulation is that they can add explicit gating in time when the self-attention is used in the decoder (when only states corresponding to already generated tokens are available for the self-attention). They can thus simulate the inductive bias for sequential processing recurrent architecture have. It is cool, but it does not influence the translation quality much, so I will not go into details.

Machine Translation

Machine translation is among the task they evaluate the method on (as well as language modeling and text classification). They match the translation quality of the standard Transformer with an almost 2 times speedup. Unfortunately, they only evaluate the BLEU score, so it is hard to say if and how this change affects the translations, but I would expect that not at all.

In the end, what we get is a faster model with a smaller carbon footprint. (Or an opportunity to train larger models at the same CO₂ cost.) And the greatest thing is that the only needed was a little bit of calculus and linear algebra, rather than infinite hours of computation time.

Update on 20.03.2021 after a brief discussion with Leo Boytsov:

Although the paper reports a 2× speedup on MT, the memory savings are probably not as large they may seem at first. Let $M$ be the input length, $d$ model dimension and also the dimension of the output of the random function $\phi$. In Section 3.4, they say they standard attention need approx. $Md$ memory, the random feature atdention needs $4d + 2d^2$. With $d$ being typically 512, this means that the memory savings start for $M > 2d$, i.e., for inputs with thousands of tokens, much longer than usually in MT.