This week, it will be the third time in recent weeks when I am going to review a paper that primarily focuses on unsupervised machine translation. The title of the paper is A Multilingual View on Unsupervised Machine Translation and it describes again work done at Google. The paper presents a probabilistic formalism for unsupervised MT and using that formalism it shows how to use parallel data between two languages if you actually want to translate into a third one.

I like this paper because it seems to me that it is an important step to what I see as one of the long-term goals of machine translation—having a single large model that we will feed with all data available: bilingual, monolingual, multilingual, whatever we have, that will learn to translate between all available pairs. For every low-resource language, there are certainly several high-resource languages the low-resource one can benefit from. For distant languages that seem to conceptualize the world significantly differently, there is a continuum of mutually related languages that allow mutual grounding of the concepts via more similar conceptual schemes.

Standard supervised machine translation is trained using a parallel corpus, a long list of sentence pairs which are mutual translation and this works pretty well if we have enough data. In addition to that, several interesting research directions deal with situations when we only have little available, different data that we actually want or no data at all. These are mainly:

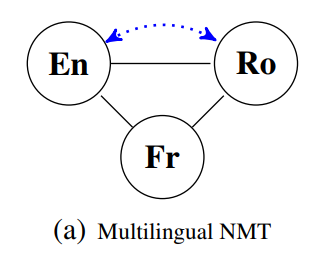
Multilingual translation. In this case, we have parallel data for all languages, but for some of the languages, we have less data than for the others. A single model for multiple languages can reuse what it learned in a high-resourced language for a similar low-resourced language as we saw for instance in the case of Google’s Massively Multilingual MT or Facebook’s recent experiments with translation between English and Nepali which largely benefited from using Hindi data. For the language triplet of English, French, and Romanian it would look like this: (Figure 1a on page 1 of the paper):

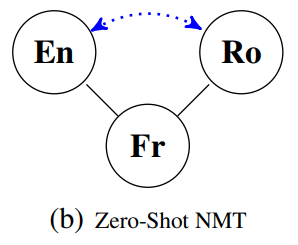
Zero-shot translation. We talk about zero-shot translation when we train a single system for translation from A to B and from B to C. If we do it cleverly, the model should also be able to translate from A directly to C without seeing this language pair during training at all. However, it seems hard to make such a system to work better than a cascade of two systems. (I already discussed this topic in MT Weekly 7.) For the same languages as in the previous figure, it can look like this (Figure 1b of the paper):

Unsupervised translation. In this setup, we only have monolingual data for both languages, but no parallel data at all. I have discussed this topic already in MT Weekly 26 and 28.

This paper adds other interesting setups:

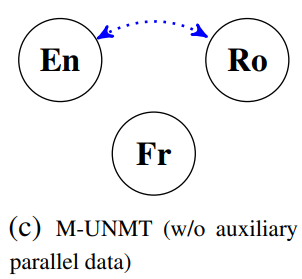
• We want to translate between A and B, we do not have any parallel data for A and B, but we have additional monolingual data for C (Figure 1c of the paper).

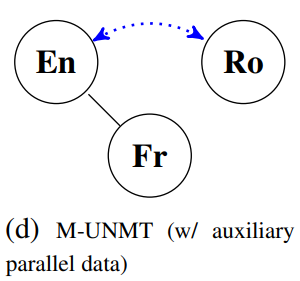
• We want to translate between A and B, we do not have any parallel data for A and B, but you have bilingual data between A and C (Figure 1d of the paper).

They only experiment with language triplets, but their method seems to generalize for arbitrarily many languages.

First of all, they formalize unsupervised translation training using back-translation, so they can formulate it as the expectation-maximization algorithm.

We need two things to use the algorithm: a parameterized model and some data. This good old unsupervised learning algorithm operates iteratively in two steps:

1. Expectation: Find out what effect would the current model parametrization on the data. In other words, annotate the data with the current model. This is what you expect with the current model.

2. Maximization: Use the annotated data to update your model, so you make what you expect more probable.

This is guaranteed to converge, but not guaranteed to learn anything interesting. Imagine, you have an image classifier, you annotate your data with the classifier and learn a new classifier on that data. The new classifier will likely be exactly the same as the old one. The expectation-maximization algorithm will converge, probably after a single step, but not learn anything useful.

A typical application of this algorithm is vector clustering. We have a set of vectors that form some groups that are unknown to us and we want to discover them. Each cluster is represented with one centroid and each vector in our dataset belongs to a cluster defined by the closest centroid. The algorithm does the following:

1. Expectation: For each vector, compute to which centroid it belongs. This gives us a better clustering than in the previous step because we just correctly classified the vectors given the centroids.

2. Maximization: Compute new centroid positions that better reflect how the vectors are currently labeled. This also makes the clustering better because now the centroids better fit the clusters.

Every step thus improves the clustering, until it converges, as you can see on an illustration from Wikimedia Commons:

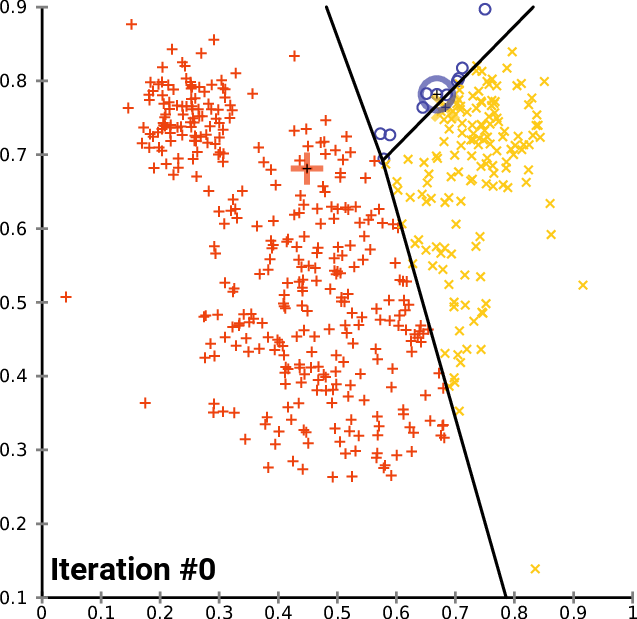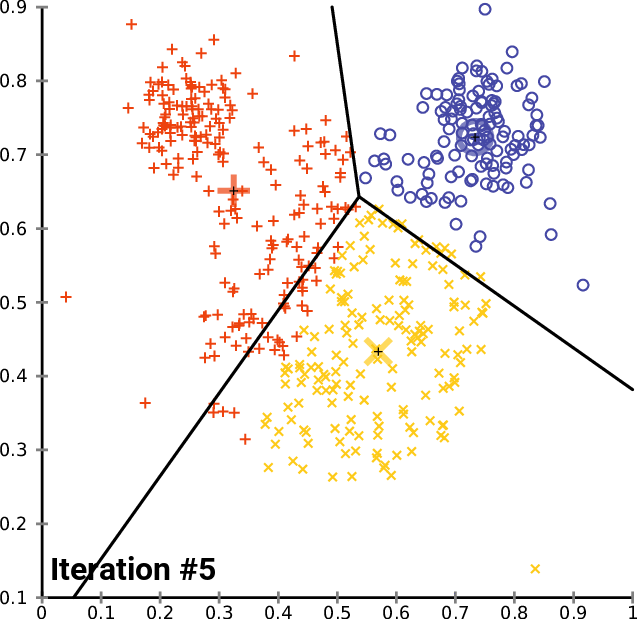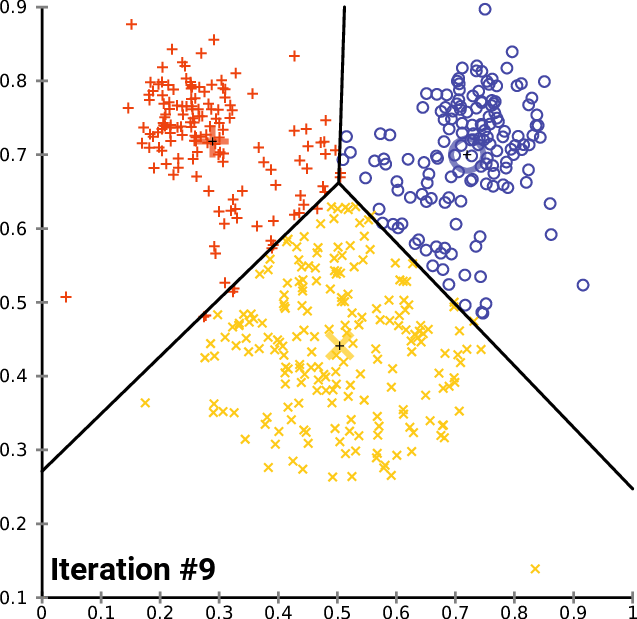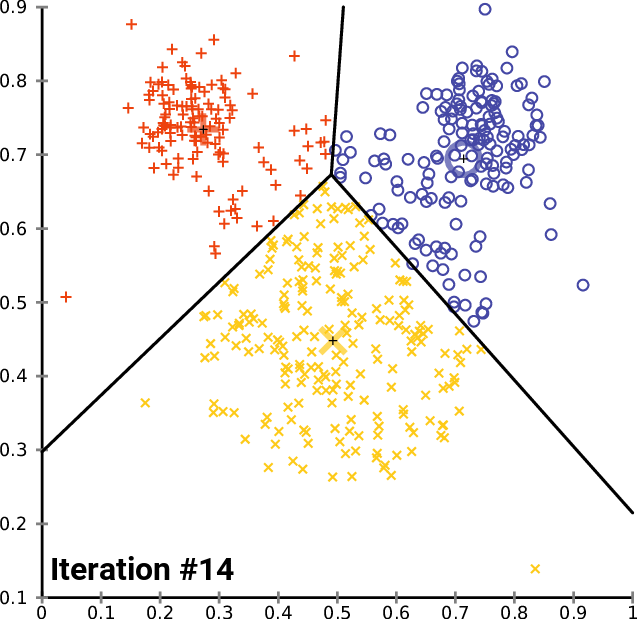
In unsupervised machine translation, the expectation-maximization is used similarly. We have two translation models for translation from A to B and from B to A.

1. Expectation: Translate monolingual data with current models, i.e., find some good translation pairs given the model and generate synthetic source side for monolingual texts.

2. Maximization: Maximization: Update the models such that the translation pairs become more probable.

In the paper, they do a math exercise with expected values and conditional probabilities and show that if we want to optimize the translation probabilities $p(a|b)$ and $p(b|a)$ where sentences $a$, $b$ are drawn randomly from an unobservable distribution of translation pairs $(a, b) \sim (A, B)$, we end up with terms that actually describe the back-translation in such a way that we can optimize them with expectation-maximization algorithm.

Pretty much nothing changes when they add a third language. They end up with an equation that contains back-translation terms for all pairs of languages. This is of course intuitively clear, but it is nice to have it formalized.

In the next step, they do similar math for adding parallel data between some languages. We can surely directly maximize the probability for translation in the two directions for which we have the parallel data, but this theoretical framework, we can infer additional loss that they call the cross-translation term and we can imagine it as a kind of consistency loss. If we have the parallel sentence pairs, they should have the same translations into the third language.

In the experimental part, they first pre-trained a denoising autoencoder for all the languages (similarly to what I discussed in MT Weekly 28) and then they finetune it using the presented approach.

Without the auxiliary data, they reach slightly worse results than MASS (pre-trained bilingual autoencoder tuned by iterative back-translation) which is a surprise for me because the pre-training is the same and the back-translation procedure is almost the same. However, they can show a clear gain from using the auxiliary parallel data.

Adding the auxiliary language pair seems to add consistently around 3 BLEU points for all language pairs they tried. Experiments with different auxiliary languages show that language relatedness matters (Romanesque languages help to improve translation into Romanian whereas Czech does not). Unfortunately, they did not try using multiple auxiliary language pairs. I would be very interested in seeing if this only the amount of auxiliary data that helps or if a larger variety of language phenomena in the data could help.

I already said what I liked on the paper, but there are also obvious drawbacks to this method. When we would apply this method on many languages at once, with parallel data only for few pairs, most of the updates of the model will be unsupervised or using the cross-translation term which is probably not the most efficient use of the parallel data that provide the model the strongest supervision. And I must add my usual objection: training a massively multilingual system under this setup will be extremely computationally expensive and out of reach of most research labs in the world. (I admit it is easy to criticize, but hard to invent something that does not need so many resources).