This week’s post contains more math than usually. I will talk about a paper that unifies several decoding algorithms in MT using one simple equation. The paper is called A Generalized Framework of Sequence Generation with Application to Undirected Sequence Models, it comes from New York University and appeared on arXiv a month ago.

People utter words one by one linearly in time, they write left-to-right (or in other consistent direction), but researchers in natural language processing obviously got bored of it and try to come up with models that generate sentences in any thinkable order, just not left-to-right. We already talked about bidirectional decoding, there are insertion-based models, models generating all words in parallel. A brand new pre-trained contextual word representation XLNet (rest in peace, dear BERT) considers all possible orders (all permutations) in which a sentence can be generated. It is no wonder that the authors of the generalized sequence generation framework wanted to organize this mess a little bit and wrote down an equation that can describe almost all existing ways how sequences can be generated.

Left-to-right models still provide state-of-the-art translation quality. From preprints I have seen on arXiv, it seems that all submissions to the WMT competition are based on auto-regressive Transformers. Nevertheless, researchers around the world put a huge effort into alternative ways of sentence generation. So, there must something about it if they try so hard.

Let’s have a look at the equation and start with some notation:

• X is an input sentence in the source language.

• L is the length of the target sentence.

• T is a number of steps in which the decoder operates. If we generated the sentence left-to-right, it would be T=L. If the sentence is generated non-autoregressively, T=1. Non-autoregressive models with iterative refinement (as the one I wrote about a few weeks ago) use a small constant number steps, e.g., T=10.

In the formalism, generating a sequence can be described as a sequence of edit operation (z, y) which mean insert/rewrite symbol y at position z. For example “(0, A), (1, B), (2, C), (3, D)” will generate sequence ABCD. In each step (t) of the decoding, multiple operations can be made.

And here is the magical equation:

G is the sequence of edit operation (the thing we are interested in – the decoding process), Y^≤t is a set of symbols used until step t, Z^t is a set of positions that were edited in step t.

Let’s start with the first term:

This is a prediction of how many words the target sentence will have. It assigns a probability to all integers from 1 to some large enough value.

Now have a look at the product signs:

This means that in each decoding step t+1, we take each word in the target sentence from i to L and either do something with the position (z_i=1) or not (z_i=0).

First, we have a look at the probability that we will edit the token at position i.

Interestingly, using this probability function, we can easily simulate left-to-right decoding – at step t just assign a probability of 1 to the word on t-th position, zero to the rest and that is it. When we actually decode from the model, we need to decide (or sample) based on the probability of whether z should be set to 0 or 1 because we eventually need to make an edit operation or do nothing (because we just don’t have quantum sentences). We can always choose one position and decode the sentence token by token, or multiple positions and decode in parallel.

The last term is a probability distribution over the target language vocabulary:

Assuming I already know I want to edit at position i (i.e., z_i^t+1 = 1), this distribution tells me scores for symbols that can be used at the particular position. The decoding algorithm might take only the single best-scoring token, or alternatively, it can keep multiple best-scoring options and use them in a beam search.

And finally, we have the exponent in the equation. If the algorithm decides not to edit at position i, z_i^t+1 gets the value of zero, this will make the last term equal to 1 and it will not influence the result of the large products because it does not matter what probability a token has if we do not use it anyway.

We have the equation, now we need to find a model architecture that would allow such decoding. And for this, the authors used an excellent work by Facebook AI from this January called Cross-lingual Language Model Pretraining. The paper describes several ways of training cross-lingual language representation that can be used for cross-lingual tasks including machine translation.

The basic idea is quite straightforward and can be seen from this image:

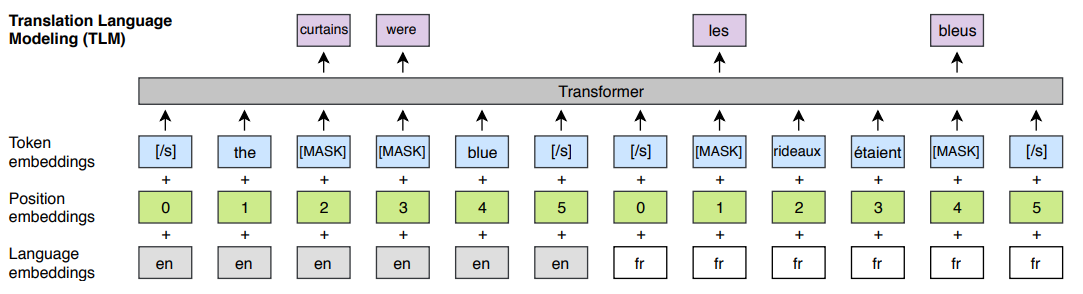
(image is taken from Figure 1, page 4, Lample and Conneau: Cross-lingual Language Model Pretraining)

They just concatenate parallel sentences in two languages, mask some words, apply a stack of Transformer layers and predict what the masked-out words were. (They basically do the same thing and BERT but on two parallel sentences).

Now, when we have such a trained model and equation that can describe the decoding in general terms, we can start discussing the decoding. Probabilities p(y^t+1|…) are already trained with the model, the remaining thing to play with is probability p(z^t+1|…) which is not trained from the data, but hand-designed based on properties of distributions p(y^t+1|…). We can sample positions uniformly, prefer positions which are easy to estimate (distribution p(y^t+1|…)) has a low entropy), replace tokens which have the lowest probability, left-to-right, etc. All strategies that are not entirely stupied (e.g., generated the most difficult words first) perform similarly well. My guess is that we can soon expect someone inventing decoding strategies learned from data.

The killer feature is that you can use the same model both for linear-time and constant-time (non-autoregressive) decoding. And they both work remarkably well. For linear time decoding (word by word), the translation quality of basically the same as the current best autoregressive model. The constant time decoding is only 2 BLEU points worse than left-to-right, which actually makes the model quite appealing for practical use because offers a decent trade-off translation quality and latency.

BibTeX Reference

@article{mansimov2019generalized,
  author    = {Elman Mansimov and
               Alex Wang and
               Kyunghyun Cho},
  title     = {A Generalized Framework of Sequence Generation with Application to
               Undirected Sequence Models},
  journal   = {CoRR},
  volume    = {abs/1905.12790},
  year      = {2019},
  url       = {http://arxiv.org/abs/1905.12790},
  archivePrefix = {arXiv},
  eprint    = {1905.12790},
}